Part 7 - Introduction to the B-Tree

The B-Tree is the data structure SQLite uses to represent both tables and indexes, so it’s a pretty central idea. This article will just introduce the data structure, so it won’t have any code.

Why is a tree a good data structure for a database?

Searching for a particular value is fast (logarithmic time)
Inserting / deleting a value you’ve already found is fast (constant-ish time to rebalance)
Traversing a range of values is fast (unlike a hash map)

A B-Tree is different from a binary tree (the “B” probably stands for the inventor’s name, but could also stand for “balanced”). Here’s an example B-Tree:

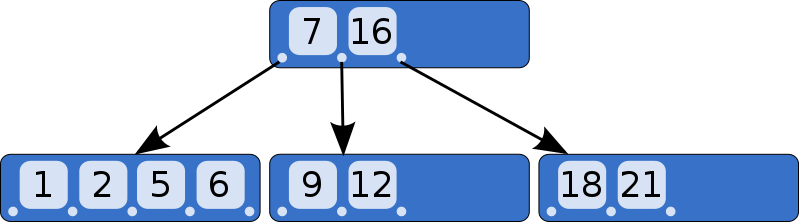example B-Tree (https://en.wikipedia.org/wiki/File:B-tree.svg)

Unlike a binary tree, each node in a B-Tree can have more than 2 children. Each node can have up to m children, where m is called the tree’s “order”. To keep the tree mostly balanced, we also say nodes have to have at least m/2 children (rounded up).

Exceptions:

Leaf nodes have 0 children
The root node can have fewer than m children but must have at least 2
If the root node is a leaf node (the only node), it still has 0 children

The picture from above is a B-Tree, which SQLite uses to store indexes. To store tables, SQLites uses a variation called a B+ tree.

	B-tree	B+ tree
Pronounced	“Bee Tree”	“Bee Plus Tree”
Used to store	Indexes	Tables
Internal nodes store keys	Yes	Yes
Internal nodes store values	Yes	No
Number of children per node	Less	More
Internal nodes vs. leaf nodes	Same structure	Different structure

Until we get to implementing indexes, I’m going to talk solely about B+ trees, but I’ll just refer to it as a B-tree or a btree.

Nodes with children are called “internal” nodes. Internal nodes and leaf nodes are structured differently:

For an order-m tree…	Internal Node	Leaf Node
Stores	keys and pointers to children	keys and values
Number of keys	up to m-1	as many as will fit
Number of pointers	number of keys + 1	none
Number of values	none	number of keys
Key purpose	used for routing	paired with value
Stores values?	No	Yes

Let’s work through an example to see how a B-tree grows as you insert elements into it. To keep things simple, the tree will be order 3. That means:

up to 3 children per internal node
up to 2 keys per internal node
at least 2 children per internal node
at least 1 key per internal node

An empty B-tree has a single node: the root node. The root node starts as a leaf node with zero key/value pairs:

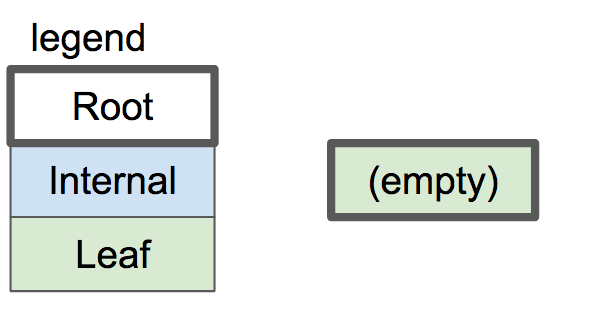empty btree

If we insert a couple key/value pairs, they are stored in the leaf node in sorted order.

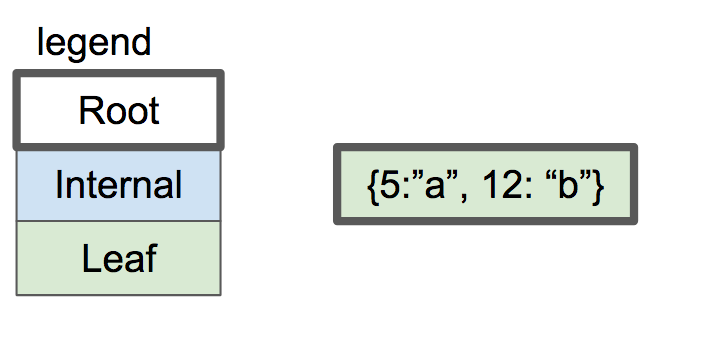one-node btree

Let’s say that the capacity of a leaf node is two key/value pairs. When we insert another, we have to split the leaf node and put half the pairs in each node. Both nodes become children of a new internal node which will now be the root node.

two-level btree

The internal node has 1 key and 2 pointers to child nodes. If we want to look up a key that is less than or equal to 5, we look in the left child. If we want to look up a key greater than 5, we look in the right child.

Now let’s insert the key “2”. First we look up which leaf node it would be in if it was present, and we arrive at the left leaf node. The node is full, so we split the leaf node and create a new entry in the parent node.

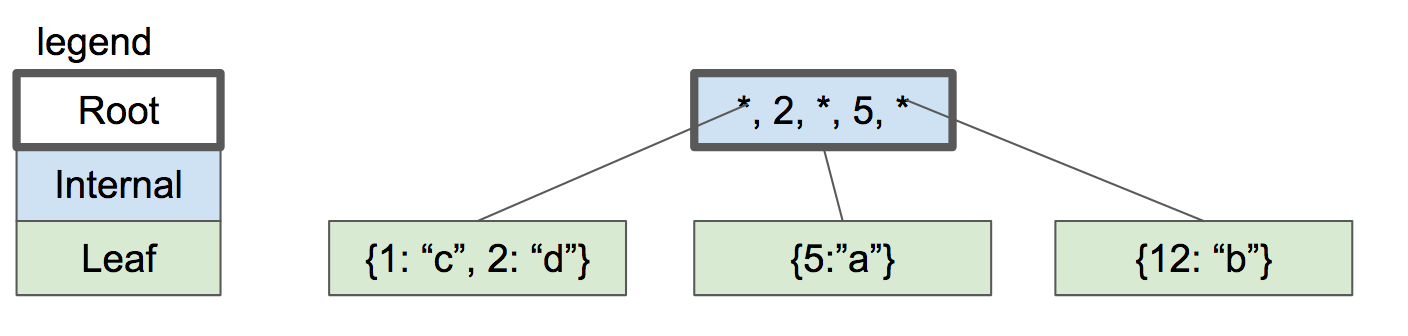four-node btree

Let’s keep adding keys. 18 and 21. We get to the point where we have to split again, but there’s no room in the parent node for another key/pointer pair.

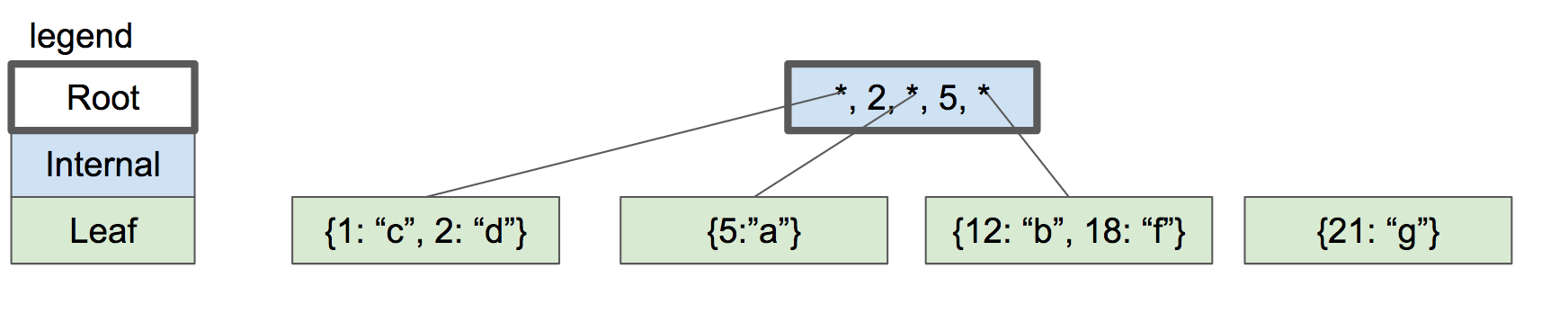no room in internal node

The solution is to split the root node into two internal nodes, then create new root node to be their parent.

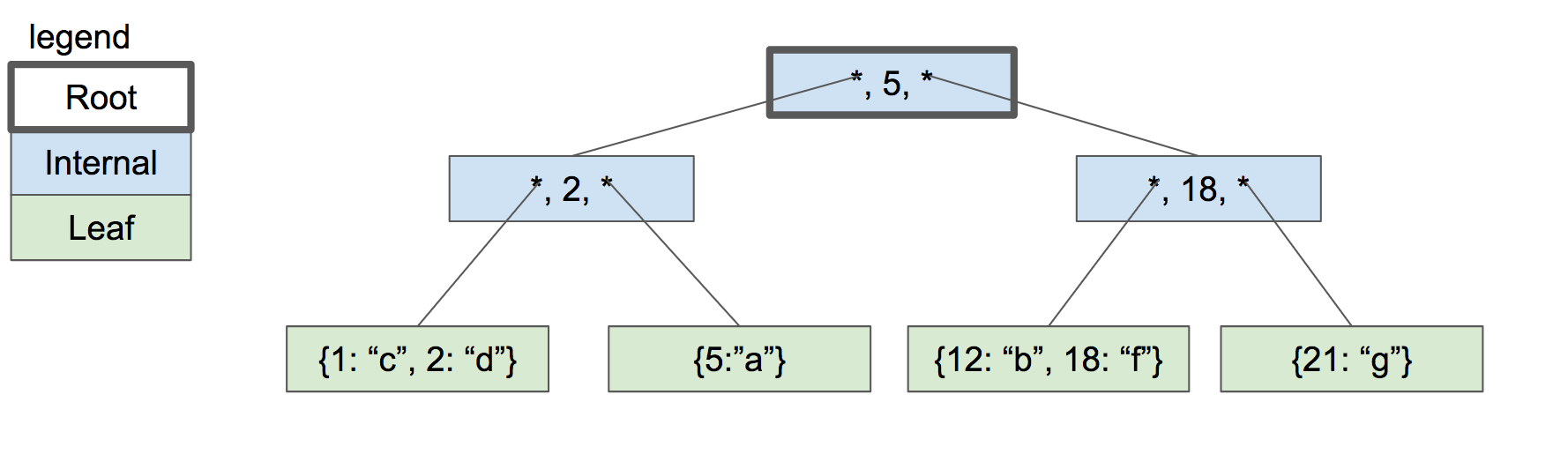three-level btree

The depth of the tree only increases when we split the root node. Every leaf node has the same depth and close to the same number of key/value pairs, so the tree remains balanced and quick to search.

I’m going to hold off on discussion of deleting keys from the tree until after we’ve implemented insertion.

When we implement this data structure, each node will correspond to one page. The root node will exist in page 0. Child pointers will simply be the page number that contains the child node.

Next time, we start implementing the btree!

Part 6 - The Cursor Abstraction

Part 8 - B-Tree Leaf Node Format